Summary
I am primarily interested in symbolic computation, numerical real algebraic geometry, validated computing, and optimization. I am also interested in techniques for integrating technology in to the classroom. I have a separate page set up where I discuss these topics in more depth.
For students that are interested in doing research, check out the student research page to see what other students of mine have worked on in the past. One topic that is easily accessible to students is recreational mathematics. In particular, I have a series of projects that involve developing algorithmic strategies for board games.
Publications
| Year | Title |
|---|---|
| 2014 | Solving the continuous nonlinear resource allocation problem with an interior point method
 Abstract: The sparsity and algebraic structure of convex resource allocation problems have given rise to highly specialized methods. We show that the sparsity structure alone yields a closed-form Newton step for the generic primal-dual interior point method. Computational tests indicate that this makes the interior point method competitive with the leading special-purpose method on several important problem classes for which the latter can exploit additional algebraic structure. Moreover, the interior point method consistently outperforms the specialized method when no additional algebraic structure is used or available. Abstract: The sparsity and algebraic structure of convex resource allocation problems have given rise to highly specialized methods. We show that the sparsity structure alone yields a closed-form Newton step for the generic primal-dual interior point method. Computational tests indicate that this makes the interior point method competitive with the leading special-purpose method on several important problem classes for which the latter can exploit additional algebraic structure. Moreover, the interior point method consistently outperforms the specialized method when no additional algebraic structure is used or available.Cite: Stephen E. Wright, James J. Rohal, Solving the continuous nonlinear resource allocation problem with an interior point method, Operations Research Letters, Volume 42, Issues 6–7, September 2014, Pages 404-408, ISSN 0167-6377, http://dx.doi.org/10.1016/j.orl.2014.07.001.
|
Connectivity in Semi-Algebraic Sets
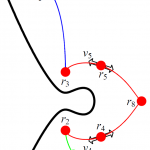 Abstract: A semi-algebraic set is a subset of real space defined by polynomial equations and inequalities and is a union of finitely many maximally connected components. In this thesis we consider the problem of deciding whether two given points in a semi-algebraic set are connected; that is, whether the two points lie in the same connected component. In particular, we consider the semi-algebraic set defined by f = 0 where f is a given polynomial. The motivation comes from the observation that many important or non-trivial problems in science and engineering can be often reduced to that of connectivity. Due to its importance, there has been intense research effort on the problem. We will describe a symbolic-numeric method for solving this problem based on gradient ascent. In the first part of this thesis we will describe the symbolic part of the method. In a forthcoming second paper, we will describe the numeric part of the method. The second part of this thesis focuses on proving the partial correctness and termination of the symbolic method assuming the correctness of the numeric part. In the third part of the thesis we give an upper bound on the length of a path connecting the two input points if they lie in a same connected component. In the last part of the thesis we give experimental timing results for the symbolic-numeric method. Abstract: A semi-algebraic set is a subset of real space defined by polynomial equations and inequalities and is a union of finitely many maximally connected components. In this thesis we consider the problem of deciding whether two given points in a semi-algebraic set are connected; that is, whether the two points lie in the same connected component. In particular, we consider the semi-algebraic set defined by f = 0 where f is a given polynomial. The motivation comes from the observation that many important or non-trivial problems in science and engineering can be often reduced to that of connectivity. Due to its importance, there has been intense research effort on the problem. We will describe a symbolic-numeric method for solving this problem based on gradient ascent. In the first part of this thesis we will describe the symbolic part of the method. In a forthcoming second paper, we will describe the numeric part of the method. The second part of this thesis focuses on proving the partial correctness and termination of the symbolic method assuming the correctness of the numeric part. In the third part of the thesis we give an upper bound on the length of a path connecting the two input points if they lie in a same connected component. In the last part of the thesis we give experimental timing results for the symbolic-numeric method.Cite: James J. Rohal. Connectivity in Semi-Algebraic Sets. Dissertation, North Carolina State University. Ann Arbor: ProQuest/UMI, May 12, 2014.
|
Talks / Posters
Unpublished Notes
| Year | Title |
|---|---|
| 2009 | On the Solution to the Nonlinear Resource Allocation Problem Using Variable Fixing and Interior-Point Methods
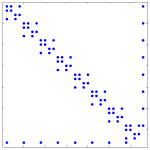 Abstract: We exploit the sparsity and algebraic structure of the convex resource allocation problem to derive a method that is competitive with previous solutions. The method makes use of the sparsity structure in the Newton step of an interior point method, with the addition of Tapia indicators. Numerical results comparing the methods are included. More info. Abstract: We exploit the sparsity and algebraic structure of the convex resource allocation problem to derive a method that is competitive with previous solutions. The method makes use of the sparsity structure in the Newton step of an interior point method, with the addition of Tapia indicators. Numerical results comparing the methods are included. More info.
|
| 2007 | The SIAM 100.0000000-Digit Challenge: A Study In High Accuracy Numerical Computing Using Interval Analysis and Mathematica
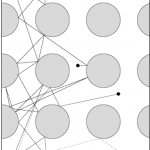 Abstract: This Independent Study concerns itself with computational mathematics with an emphasis on three specific problems posed during the SIAM 100-Dollar, 100-Digit Challenge. The difficulty of the challenge is solving the problems with enough precision to get answers accurate to 10 digits. Most solutions put forth by contestants offered no proof of correctness for their answers. By using theory from the field of interval analysis, it will be possible to develop algorithms that will provide a solution within a desired accuracy and that is verifiably correct. To do so, I will be implementing these algorithms in Mathematica and using interval analysis to create computer-assisted proofs for the solutions. More info. Abstract: This Independent Study concerns itself with computational mathematics with an emphasis on three specific problems posed during the SIAM 100-Dollar, 100-Digit Challenge. The difficulty of the challenge is solving the problems with enough precision to get answers accurate to 10 digits. Most solutions put forth by contestants offered no proof of correctness for their answers. By using theory from the field of interval analysis, it will be possible to develop algorithms that will provide a solution within a desired accuracy and that is verifiably correct. To do so, I will be implementing these algorithms in Mathematica and using interval analysis to create computer-assisted proofs for the solutions. More info.
|
| 2006 | Self-Similar Tilings of Nilpotent Lie Groups
 Abstract: We construct self-similar fractal tilings on rationally graded nilpotent Lie groups. Specific examples and graphs of fractal tilings in the Heisenberg group are given. More info. Abstract: We construct self-similar fractal tilings on rationally graded nilpotent Lie groups. Specific examples and graphs of fractal tilings in the Heisenberg group are given. More info.
|