Below are a sample of the activities I do in my mathematics classes. I embrace technology and use tools such as Mathematica and Maple in the classroom. The dynamic interactivity and visualization offered by these computer packages cannot be duplicated on a chalkboard. For example, I created the animation below in Mathematica to illustrate how rotation matrices are used in computer graphics.
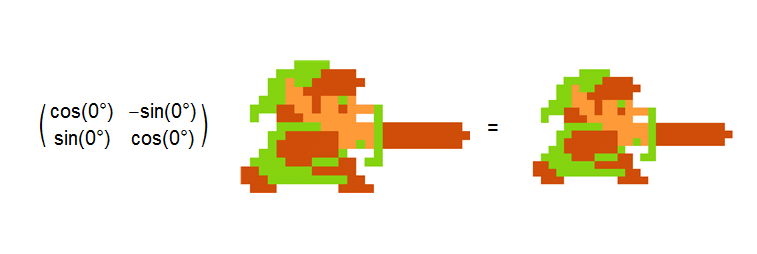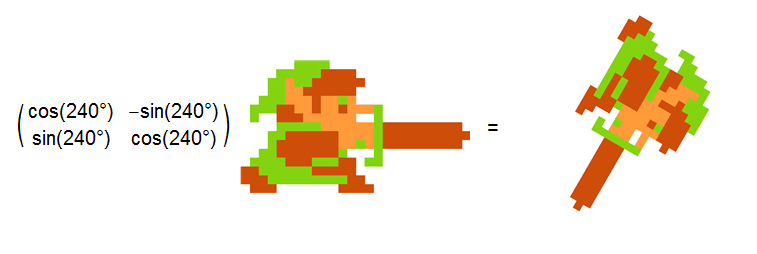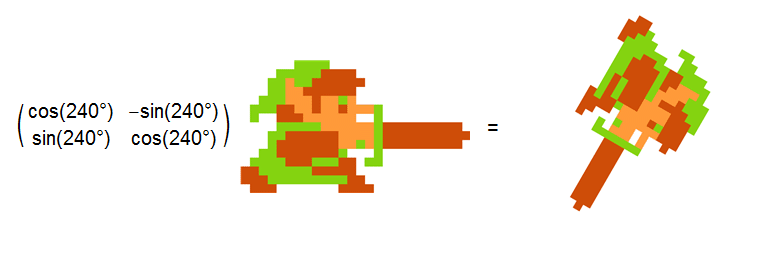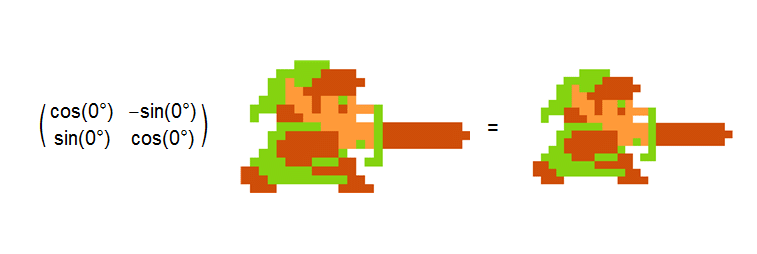
I also take an active learning approach in all of my classes. By interactively engaging with the students, I can challenge them to think or to do something that requires thought and provide immediate feedback. Research has shown that students typically do better in classrooms that use interactive engagement than those that perform traditional lectures.
Projects
For my Calculus I courses at Miami University, I gave a writing assignment each semester. The first project gave students the opportunity to create their own math problem. This assignment was created to improve skills that one does not learn in the classroom. For example, it taught students how to write precisely and concisely and to describe their ideas neatly. The second project was a semester long experiment in math blogging. Students had to submit several posts to the blog which were either small problems with a solution, or talked about one of the listed topics. At the time, blogging about mathematics was gaining traction and this seemed like an excellent opportunity to improve my students’ writing abilities. Extra credit was given to those students who tried to use \(\LaTeX\).
For my Calculus II course at West Liberty University, I asked students to create a video presentation of themselves explaining a solution to a fluid force problem, an application of integration. The project helped illustrate to the students the importance of communicating mathematics to others. Students found this project enjoyable, but many were quite nervous in front of a camera!
The final for Computer Programming for the Sciences, an introductory programming class at West Liberty University, is a large project that requires students to create a gradebook programmatically given an Excel sheet filled with data. The project used many of the concepts discussed during the semester and was guided by hints in the project description.
In my Numerical Analysis course at West Liberty, I gave several programming assignments. For example, here are the first and second assignments. Each assignment expands on ideas discussed in class and requires students to submit Mathematica code. To minimize the cost, I had students use the Wolfram Programming Cloud, a free (ableit slow) version of Mathematica that is available in the browser.
In my Topology course at West Liberty University I am taking a discovery learning approach. Each student is given a specific topology, which is their “baby” for the semester. For example, this semester I am using the trivial, discrete, finite complement, standard, upper limit, and lower limit topologies. When we discuss a topic in class, such as separation axioms, I will ask the students to discover what axioms their “baby” topological space satisfy. I also have students create a typed dictionary of theorems and definitions that they update weekly to improve their \(\LaTeX\) abilities. In the future, I plan to make a series of projects that will involve the forward and inverse kinematics problems, with the ultimate goal of introducing Gröebner bases and the Cylindrical Algebraic Decomposition. A draft of the project introduction is available.
Labs
In Calculus II I experimented with labs in both Mathematica and Maple. The Mathematica worksheets were self contained.
- Introduction to Mathematica [.nb]
- Integration Strategies [.nb]
- Approximate Integration [.nb]
- Differential Equations [.nb]
With some of the Maple worksheets I included an instructional video that helped explained some of the syntax.
- Approximate Integration [.mw]: Video
- Differential Equations [.mw]: Video
- Euler’s Method [.mw]: Video
- Homogeneous Second-Order Differential Equations [.mw]: Video
- Non-Homogeneous Second-Order Differential Equations [.mw]: Video
I believe a future improvement would be the inclusion of automated grading of these labs with immediate feedback. You can read more about this over at my research page.
Instructional Technology
I experiment with various instructional technologies in my classes with the goal being to increase student engagement. A simple application of technology in my classes is using recording software to save my lectures. In some classes I recorded the doc cam I used, in others I used a tripod mounted video camera to record my lecture, while in some classes I recorded the screen during a PowerPoint presentation. I upload these lectures to YouTube so the students can watch them later at their leisure. Ideally, these videos could be used to support an online class in the future. I am also interested in what makes a “good” video. I discuss this more in my research page.
The slides I create in PowerPoint, Keynote, and Beamer are dynamic and rich. I focus on presenting only the essential information and making the concepts easy to understand through animations and visualizations. When I create slides, such as this one for introducing series in Calculus II, I usually create a pair of skeleton notes to hand to the class. By doing so, I can create a guided learning experience where students are actively engaged.
I pair my PowerPoint presentations with other technologies, such as a writing tablet or a computer algebra system. For example, in my Numerical Analysis class, I paired my PowerPoint presentation with a wireless Wacom Intuos tablet and was able to annotate my presentation as I walked around the room. I felt that students were more engaged as I paced the room as opposed to being tethered to a computer desk. Many of my lectures are peppered with interactive Maple and Mathematica demos. For instance, in my Precalculus class I use Mathematica demonstrations to illustrate transformations of sine and cosine functions. In the future, I plan to publish these interactive activities on the Wolfram Demonstrations site. An instance where I use Maple is in my Calculus II class where I can easily visualize solids of revolution in 3D as well as the associated slices.
Course List
| Year | Short Name | Full Name | Location | Size |
| Spring 2016 | MATH 145-01 | Pre-Calculus | West Liberty | 9 |
| MATH 145-02 | Pre-Calculus | West Liberty | 22 | |
| MATH 160-02 | Introduction to Statistics | West Liberty | 16 | |
| MATH 175-01 | Computer Programming for the Sciences | West Liberty | 9 | |
| Fall 2015 | MATH 145-01 | Pre-Calculus | West Liberty | 35 |
| MATH 145-02 | Pre-Calculus | West Liberty | 11 | |
| MATH 160-01 | Introduction to Statistics | West Liberty | 36 | |
| MATH 373-01 | Finite Mathematics | West Liberty | 11 | |
| MATH 478-01 | Topology | West Liberty | 6 | |
| Spring 2015 | MATH 145-01 | Pre-Calculus | West Liberty | 21 |
| MATH 175-01 | Computer Programming for the Sciences | West Liberty | 10 | |
| MATH 280-01 | Mathematics Seminar | West Liberty | 4 | |
| MATH 475-01 | Numerical Analysis | West Liberty | 9 | |
| Fall 2014 | MATH 145-01 | Pre-Calculus | West Liberty | 10 |
| MATH 145-02 | Pre-Calculus | West Liberty | 8 | |
| MATH 211-01 | Calculus II | West Liberty | 17 | |
| Spring 2014 | MA 241-009 | Calculus II | NC State | 50 |
| Fall 2013 | MA 242-001 | Calculus III | NC State | 110 |
| Spring 2013 | MA 241-006 | Calculus II | NC State | 103 |
| Fall 2012 | MA 242-009 | Calculus III | NC State | 52 |
| Summer 2012 | MA 242-003 | Calculus III | NC State | 12 |
| Fall 2011 | MA 242-001 | Calculus III | NC State | 116 |
| Fall 2010 | MA 242-013 | Calculus III | NC State | 13 |
| Spring 2009 | MTH-151N | Calculus I | Miami | 30 |
| Fall 2008 | MTH-104C | Pre-Calculus | Miami | 33 |
| Spring 2008 | MTH-151T | Calculus I | Miami | 26 |
| Fall 2007 | MTH-104F | Pre-Calculus | Miami | 31 |