We will be studying three problems that show up in the field of robotics: the forward kinematics problem, the inverse kinematics problem, and the motion planning problem. We illustrate these problems with several interactive demonstrations. We will give more precise descriptions of these problems in the later sections of this project.
To run these demonstrations, you must install the Wolfram CDF plugin. After installing the plugin, restart your browser and revisit this page. To activate a demonstration, simply click on the preview image. Keep in mind that not every picture is an interactive demonstration! Depending on your browser, you may get a popup asking for your permission to run the CDF plugin.
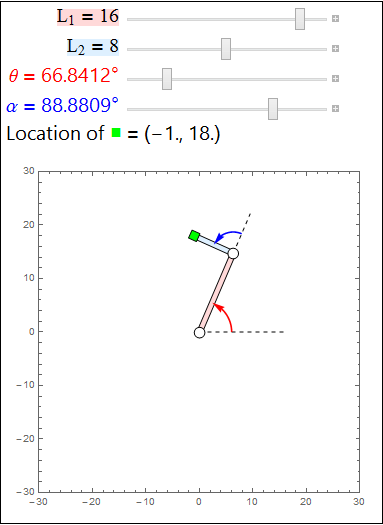
Click the image to show an interactive demonstration. Drag the sliders to move the arms of the robot.
In the demonstration above, we have a robot with two arms (the red and blue rectangles), two joints (the white circles), and one hand (the green square). In the forward kinematics problem, we know the lengths of the two arms, \(L_1\), \(L_2\), and the joint angles \(\theta\), \(\alpha\), of the robot (whose measures are shown as the red and blue arrows), and we wish to find the position of the end effector (the green hand, in our example).
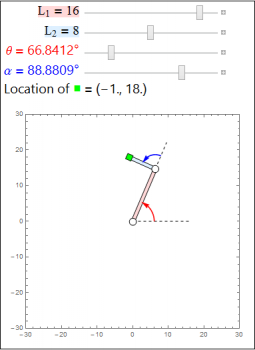
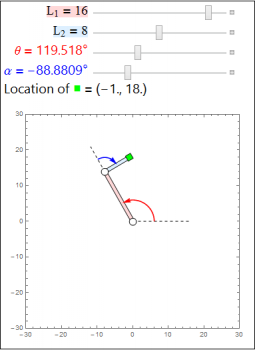
In the inverse kinematics problem, we know the position of the end effector (our hand) and the lengths of the two arms \(L_1\), \(L_2\), and we wish to find the joint angles \(\theta\), \(\alpha\) or conditions on the joint angles. Typically this is a much harder problem than the forward kinematics problem because there can be multiple choices of the joint angles which give the same hand position, as we see in the above two images.
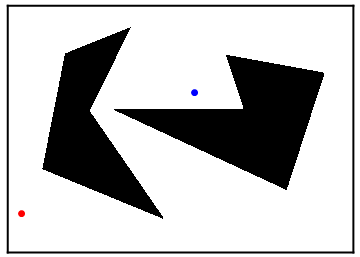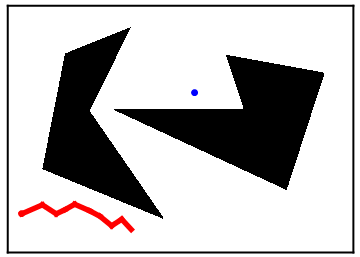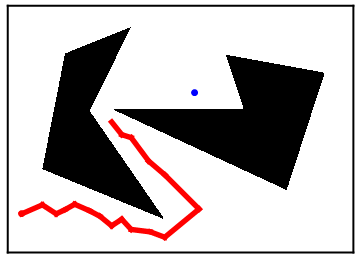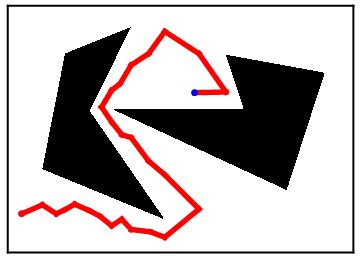
In the motion planning problem, we are given two points (denoted by the red and blue points above) and obstacles (denoted by the black polygons and black lines) and wish to determine a path connecting the two points while avoiding the obstacles (if such a path exists). One reason this problem shows up in robotics is because a robot must algorithmically determine how to navigate from a start configuration (the red point) to an end configuration (the blue point).
This project is split in to several sections. Complete all the questions in each section in order: