Below is a list of problems I have looked at with students recently. If you are interested in doing research, I have plenty of problems we can study together. Schedule a meeting and we will try to find something that you enjoy.
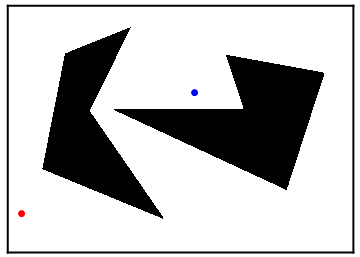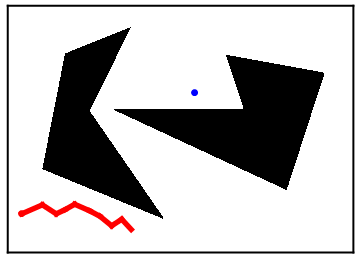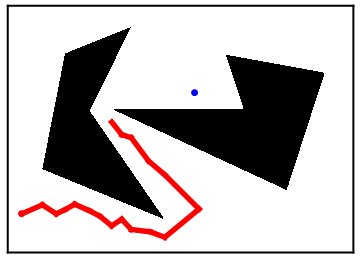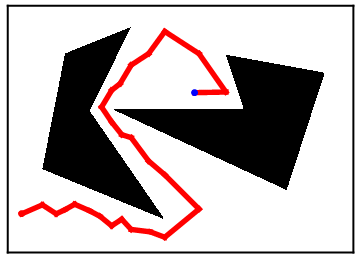
Alexis Brum [Fall 2015]Alexis is studying a version of the motion planning problem. In her case, the configuration space consists of polygonal boundaries defined by inequalities. She is developing an algorithm that discretizes the configuration space in to a graph and then applies graph search algorithms to move from a given start state to a given goal state.
Liza Jones [Fall 2015]Liza is studying a version of the PageRank algorithm used at Google. She is applying this algorithm to a webgraph consisting of nodes that are webpages from the westliberty.edu domain.
Caleb Casto [Spring 2015]Caleb studied a particular class of functions called routing functions. These functions are amenable to study in the context of determining connectivity in semi-algebraic sets. We investigated how the critical points of these functions change as you vary the parameters defining them.
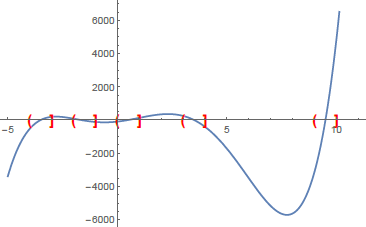
Mark Winters [Fall 2014]Mark worked on the real root isolation problem: given a polynomial f with integer coefficients, find interval bounds on all of the real roots. He helped develop a program in Mathematica that used a combination of the Budan-Fourier Theorem and results from Precalculus to solve this problem.
MacKenzie Krieger [Fall 2014]MacKenzie studied graph theory and its applicability to designing a board game. The motivation for this project came from the board game Tsuro. MacKenzie helped design a new version of the game that illustrates proper vertex colorings of graphs. The game proceeds by players alternately laying down colored pieces on each of the nodes with the rule that no two adjacent nodes can have the same color.
